------初三一轮复习之平行四边形教学实录

刘杰（江阴市利港中学江阴市蒋网健名师工作室成员）

2016年4月6号，笔者代表江阴市蒋网健名师工作室到江阴市临港实验学校上了一堂初三一轮复习《平行四边形》，现将本节课教学设计和思路、课堂实录及课后反思整理成文，与各位同行交流．

整个课堂分为3个层次，其中课堂前置任务为完成对平行四边形的定义、性质、判定的文字语言、符号语言、图形语言等自主知识建构。

【基本知识汇总】

 定义（文字语言）                图形（含图形语言）              符号语言

平行四边形

              性质                图形（含图形语言）              符号语言

边

角

对角线

对称性

 

设计解析：因为平行四边形里面的性质和判断内容较多，学生大多能基本感知，部分内容会混乱，比如：平行四边形的定义会和平行四边形判定出现“打架”；再如真命题：两组对角相等的四边形是平行四边形，学生会判别不清。因此，很有必要让学生前置完成一些基本知识，自主完成知识网络建构。

【要点梳理】

问题1．如图，□ABCD的对角线交于点O，AB＝5，AO＝3，∠ABC=50°，你能求出图中哪些线段的长和哪些角的度数？你还能得到哪些结论？

问题2．如图，四边形ABCD中，对角线AC与BD相交于点O，AB//CD．添加一个条件，使四边形ABCD是平行四边形并说明理由．

设计解析：此问为课堂唤醒学生对平行四边形判定的回顾，通过开放性案例，解决二种判定方法（含定义），自己再在黑板上画一个角，课堂上用尺规作图作出平行四边形，唤醒第三种判定方法，两组对比相等的四边形是平行四边形；最后通过追问：如图，四边形ABCD中，对角线AC与BD相交于点O，你还能添加条件，使四边形ABCD是平行四边形？唤醒对角线相等的四边形是平行四边形。

问题3：你能作一条直线把这个平行四边形面积平分吗？

（教师展示自制学具平行四边形）

生1：连接任意一条对角线．

生2：连接2条对角线，过对角线的交点任意作一条直线．

师：给出平行四边形是中心对称图形，对角线交点是对称中心．

师不停的转动平行四边形学具，问学生：这说明什么？

生：平行四边形具有不稳定性．

师：你能想象一下，这个平行四边形的对称中心运动的轨迹吗？

师：遇到一个较难的问题或陌生的问题时，要善于“退”，这里我们可以从最特殊的位置开始想象．（师不停的缓慢的转动平行四边形学具）

生：（思考后）轨迹是一个圆弧

师：刚才同学们通过老师的学具转动，初步感知了平行四边形的对称中心的轨迹是个圆弧．现在请大家一起看老师通过几何画板来演示一下，再次感悟一下．

师：同学们，当老师转动点A时，点E的轨迹是一个圆（如图1），这个圆的大小不发生变化，那么就说明，该圆一定与平行四边形中某个元素有关？你知道吗？

师：（学生长思后无法发现）同学们注意，在平行四边形转动时，有不变的元素吗？

生：（观察思考后）在平行四边形转动过程中，点E始终是线段AC的中点，取BC的中点F，连接EF，EF为△ABC的中位线，EF=12AB，

师：（再次转动平行四边形，感受以F为圆心，EF为半径的圆）如果平行四边形的两条边AB=2，BC=4，则该圆的半径是多少？

生：半径为1．

师：对吗？同学们，再观察一下，刚才老师是固定BC，拉动点A进行旋转得到点E的轨迹的．

生：半径为1或2，取CD的中点G，可以发现EG为△BCD的中位线，此时EG=2．．．

师：（继续缓慢的旋转平行四边形学具）同学们，你们观察一下，平行四边形的面积是如何变化的？

生：面积由小到大，再到小．

师：既然面积由小到大，再到小，那么一定存在面积最大的时候．

生：当变成矩形时，平行四边形面积最大．

学生练习1：已知平行四边形的周长为40，求该平行四边形面积的最大值为 ．

生：（稍加思考）100，当平行四边形变成矩形时面积最大，令其中一边为x，另一边为20－x，s=x（20－x）=－（x-10)2+100，当x=10时，面积最大值为100.

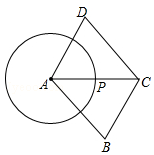
学生练习2：（2014•无锡•17）如图，已知点P是半径为1的⊙A上一点，延长AP到C，使PC=AP，以AC为对角线作▱ABCD．若AB=，则▱ABCD面积的最大值为 ．

设计解析：笔者在本课设计之处，翻阅了无锡近2年的中考试卷，注意到涉及平行四边形方面的题目走了2个极端．像2014无锡第17题，当年此题得分率很低，究其原因在于教师平时复习时忽视了四边形的稳定性，因此本课设计平行四边形不稳定时，通过几何画板发现平行四边形的对称中心的轨迹是一个圆，而且有2种可能，这里并没有跟进配套练习，原因在于课堂时间不够，其次当学生感知了轨迹是圆之后，那么像求一些定点与平行四边形对角线交点的距离最值问题，学生就可以轻松转化了．在研究平行四边形不稳定时，笔者不断转动教具，以给学生直观，轻松发现当平行四边形某个角是直角时，面积最大．学生练习1的答案100，很多学生猜出来，因此有必要让学生讲解过程，该题其实涉及2个最大值，第1为平行四边形转化为矩形时面积最大，第2为矩形面积最大时是正方形，此处解决是通过二次函数最值来解决的．熟悉的地方，停留一下，会发现不一样的风景，不一样的风景中蕴涵了美好的遐想；熟悉的图形，研究一下，会出现不一样的风景，不一样的风景中蕴涵了火热的联想．

【归类探究】

例1．（原创）如图，点E是□ABCD的边AD上一点，AE：ED=2：1，连接BE，和对角线AC交于点O，点O是AC的中点吗？如果是，请说明理由；如果不是，请求出AO：OC的值．

设计解析：本题目标是激活学生对“见平行想相似”的平行的性质运用，并串联起相似的相关内容。本题预设由学生讲解完成，并追问：你能设计一个与比值有关的问题吗？

从课堂学生反应来看，这个问题设置的还是有些问题，应该把问题的指向明确：改为“你能设计一个与面积有关的问题吗？这样学生就会联想到“同高”，更能激发学生火热联想。

例题2：（2014．铁岭改编）如图，在□ABCD中，∠ABC和∠BCD的平分线交于AD边上的一点E，若_______，则AB的长是_______．（请补充条件，设计成能求AB长度的问题）

生1：若AE=1，则AB=1

（教师追问为什么？引导学生发现AB=AE）

生2：若BC=2，则AB=1

（教师追问为什么？引导学生发现点E是中点）

生3：若BE=4，CE=3，则AB=2.5

（教师追问为什么？引导学生发现∠BEC=90°）

生4：若∠CBE=30°，CE=1，则AB=1（教师追问为什么？）

该题笔者设计的初衷为引导学生发现∠BEC=90°，并及时归纳“平行线、角平分线、等腰三角形”三兄弟的关系．

学生练习3：在平行四边形ABCD中，∠ABC和∠BCD的平分线分别交于AD于点E、F，若AB=2，EF=1，则BC=________

递进变式：（原创）如图，在平行四边形ABCD中，∠ABC和∠BCD的平分线交于AD边上的一点E，若以BC为直径的圆过点A，则△CDE的形状是

教师在学生审题后，引导学生观察“在平行四边形ABCD中，∠ABC和∠BCD的平分线交于AD边上的一点E”，你想到了什么？

生： = 1 \* GB3 ①△ABE和△CDE是等腰三角形； = 2 \* GB3 ②点E是AD的中点； = 3 \* GB3 ③∠BEC=90°；

师：“以BC为直径的圆过点A”你想到什么？

生：∠BAC=90°，

师：大胆的猜想△CDE的形状是什么？然后在小心的去求证．

生：△CDE的形状是等边三角形．连接AC，易得∠BAC=90°，因为AB∥CD，所以∠ACD=90°，在直角△ACD中，点E为AD的中点，所以CE=DE，由上面一题可以得到CD=DE，因此CD=DE =CE，所以△CDE的形状是等边三角形．

生：老师，我还有一种简单的方法．因为∠BEC=90°，所以点E也在以BC为直径的圆上，所以四边形ABCE为圆的内接四边形，所以可以得到∠ABC+∠AEC=180°，因为∠DEC+∠AEC=180°，所以∠DEC=∠ABC，在平行四边形ABCD中，∠ABC=∠CDE，∠DEC=∠CDE，进而得到CD=CE，再由刚才得到CD=DE，所以CD=DE =CE，所以△CDE的形状是等边三角形．

递进拓展：如上图，在平行四边形ABCD中，∠BEC=90°，若以BC为直径的圆过点A，AB+BC=20，sinD=0.8，则DE的长？

教师在学生审题后，引导学生关注这里的条件已经弱化，没有角平分线这个条件，只有∠BEC=90°；这里出现sinD=0.8你会产生怎样的联想？

生：因为∠BEC=90°，所以点E也在以BC为直径的圆上；sinD=0.8我联想到直角三角形，其次联想到勾3股4弦5，因此，令CD=x，则BC=AD=20－x，在直角△ACD中，由sinD=0.8，可以得到AD:CD=5:3，所以（20－x）：x=5:3，解得x=7.5，上题已证CD=CE，马上联想到三线合一，因此过点C作CH⊥AD，．．．．．．得到DE=9.

中考链接：（2015•无锡•26）已知：平面直角坐标系中，四边形OABC的顶点分别为O(0，0)、A(5，0)、

B(m，2)、C(m－5，2)．

    (1)是否存在这样的m，使得在边BC上总存在点P，使∠OPA＝90°？若存在，求出m的取值范围；若不存在，请说明理由．

(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时，求m的值．

（由于学案是提前一天下发，由题干学生发现四边形OABC为平行四边形）

由于前面的铺垫，（1）问学生很容易发现∠OPA＝90°马上联想到构圆；（2）问学生由∠AOC与∠OAB的平分线的交点Q在边BC上，马上产生∠OQA=90°，继续联想构圆，所以此题学生很轻松的就解决了．

由于课堂时间不够，此题的解答没有来得及展示，有点遗憾！下附我的解答：

解：由题可得，BC＝5，B、C两点在y＝2的直线上，直线y＝2与y轴交于点G，过A点作AH⊥BC，垂足为H，如图6，易得△OPG∽△PAH，∴eq \f(GP,OG)＝eq \f(AH,PH)，设GP＝x，则eq \f(x,2)＝eq \f(2,5－x)，解之得x＝1或x＝4．

∵P点在BC上，∴当x＝1时，得eq \b\lc\{(\a\vs3\al(m－5≤1,m≥1))，解之得：1≤m≤6；

当x＝4时，得eq \b\lc\{(\a\vs3\al(m－5≤4,m≥4))，解之得：4≤m≤9；综上可得，1≤m≤9．

(2)∵BC∥OA，BC＝OA＝5，∴四边形OABC是平行四边形．易证：∠OPA＝90°，点P在BC上，点P为BC中点．由(1)可得，P(1，2)或P(4，2)，∴m＝3.5或m＝6.5．

设计解析：片段二从最基本的“平行线、等腰三角形、角平分线”三者之间关系入手，设计条件和结论都开放性，有利于充分调动学生思维，不同层次的学生都可以参与，随着师生交流的深入，最终把关注点集中在两条角平分线集中在形成直角上，引导学生发现有隐形圆的存在，为学生见直角能联想隐蔽圆积累经验．通过针对性变式训练，强化学生见直角能联想隐蔽圆，最后利用以上积累的解题经验顺利解决2015无锡中考第26题，让学生获得一定的成就感．笔者利用这一连串递进式的变式，将学生的应具备的技能方法都罗列其中，通过师生交流，鼓励学生从题干中发现关键字词进行充分联想，让学生学会发现图形中隐藏信息，为今后遇到类似题目提供积累经验．

课堂小结，作业布置（促学生课后自主联想）

师：回想本节课内容，你能用一个词来总结吗？

生：火热的联想

师：火热的联想的前提是“敢想”，然后付之行动．大道至简，知易行难；知行合一，得到功成；大道至简，悟在天成．本课的作业：自编二题，主题1为：平行+相似+面积；主题2为：平行+角平分线．谁的题目编的好，我就以你的名字命名放到期中试卷上．

设计解析：鼓励学生敢于联想，并转化到行动上，激励学生课后自主编题，激发学生无限想象，并给一些学生创设平台，在非智力因素上去激发、引领学生的学习兴趣．

课后交流反思

1、学情预估不足，自己预设不够充分；

2、给学生思维留白时空不多；

3、给学生自主发挥（学生讲题）空间不大，由于学生讲题时，讲不到重点位置，我就显的不淡定了，多次打断学生。这些原因的出现，可能是我过于自信，上次青阳二中时，学生优秀的表现让我的课堂流畅，自己可以尽情发挥；其次，我的学案是提前让对方学校做的，我错误的预估学生肯定会很认真的做透，结果事与愿违，这说明自己的预设还是有问题。

工作室其它教师的点评对于我来说，收获点比较多，特别蒋校对我说的“平行、等腰、角平分线”三兄弟关系的自然产生启发很大，可以考虑题组。另外对于变式教学，蒋校的一个观点还是值得深思：变式的双刃性。课堂中按梯度进行不间断的变式，学生当时接受的较好，到第2天学生是否能解决，这值得商榷。如果能在另外一道题目中提炼出变式中的核心知识，这样才有效，这样的课型我自己还没有尝试过，等有机会自己设计一堂这样的课。

江阴一中钟珍玖老师的一些观点还是值得记录的：对于广泛的联想，（1）有结构的联想，比如数字的联想，这个应该就是数感的联想；（2）类比的联想，这个比较多；（3）转化思想的迁移，几何问题代数化，代数问题几何化，函数、方程、不等式之间的转化等。思维从无序到有序，这句话值得玩味！