【推荐理由】：

1. 核心素养背景下运算教学的价值探讨。

学习最终要实现知识在异质情境中的迁移。数学理解的核心是建立联系，灵活迁移。作为占数学教学内容38%左右的运算教学，需要用系统的视角，处理好认知与情感、算理和算法、结果与过程、知识与文化的关系；用长程的眼光，处理好“长线”与“短线”的关系，对数学课程进行整体性，贯通性设计，提升学生数学素养。

2. 聚焦科研，聚焦课堂的实证研究。

从2009年开始，本文作者一直聚焦“数学理解”开展挖井式研究，提出了“为理解而设计”的教育主张。本案例是基于省测中的计算问题开展的课堂实践的研究成果。

 

                                                               创设联结：破解“黑洞”

——以《两位数乘两位数的笔算》为例

江苏省江阴市教师发展中心 包静娟

一、缘起：由省测题引发的思考

课改以来,小学生的运算能力一直受到怀疑与质疑。2016年江苏省小学数学学业质量监测对理解运算意义能力的测试，安排的是这样一题（如图1）。全市学生此题的得分率为仅为60.2%，也就是说，有超过30%的学生不能将竖式中的数据与生活情境、直观点子图之间建立联系，即不能很好地理解运算的意义。

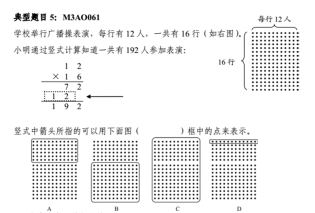2018年江苏省小学数学学业质量监测，理解运算能力的测试换成了让学生在具体情境中解释笔算除法竖式中某一步的含义，全市的得分率为62%。

两组高错误率的数据，不由引发笔者的反思，为什么能熟练计算出结果的学生却不能很好地理解运算的意义和算理呢？下面，笔者就以“两位数乘两位数的笔算”为例作一分析。

二、追因：是什么造成数学运算意义理解的能力“黑洞”？

1. 重讲授，轻体验，认知和情感产生疏离

教材中“两位数乘两位数的笔算”采用了下图的情境（如图2），即“已经放在地上10箱，还有2箱正在搬来”。这一情境具有较强的暗示性，相当于直接告知学生，计算“24×12”只要把24×10和24×2的结果相加。

由于缺失对方法多样性的甄别和选择，学生对乘法分配律存在价值的感悟是不充分的。在许多课堂上，计算方法是通过教师正面的示范讲解和学生的反复练习获得的，学生的认知差异被忽视，抽象、推理、建模的体验过程被剥夺，灌输式的学习令学习毫无智力成就的快感。

2.重算法，轻算理，规则和意义呈现割裂

计算教学常常不考虑学生的推理过程，取而代之的是一系列的规则和程序，而这些规则和程序把问题解决与意义割裂开来。许多教师并不清楚两位数乘两位数的算理，认为运算顺序与步骤就是算理，算理和算法产生混淆。在一次访谈中，有56%的老师认为：计算就是一个熟练的过程，算理讲得再清楚，学生计算时也不会去想算理，计算法则的强化训练才是最重要的。关于“竖式中第二步末尾的0为什么要舍去？”的问题调查显示，教师对计算中“位值”的理解更倾向于程序性理解，强调位值中的“位”，忽视位值中的“值”，知其然而不知其所以然，数学运算意义的理解缺少“根基”。

3. 重点状，轻结构，知识之间存在分离

“两位数乘两位数笔算”的教学，不少教师局限于就课论课，忽视它的来龙去脉，内在结构，背后的思想方法，没有与两位数乘一位数、多位数乘多位数等知识内容建立联系，没有用乘法意义、位值原理、乘法分配律等“高观点”进行统帅，情境、符号、言语、图形、操作等多种表征方式之间也呈现分离状态。这种在没有相互关联的结构基础上所获得的知识非常容易被遗忘，导致无法在复杂的情境中判断、分析和解决问题，造成了数学运算的能力“黑洞”。

三、笃行：创设联结之实践策略

数学是一个整体，不仅因为知识是纵向发展的，还因为横向之间也存在充分联系。在数学运算教学中，教师要搭建平台，在内容与内容之间，规则和意义之间，认知与情感之间，学生与学生之间创设联结，引导学生自主探索，发展数学运算素养。

1. 情境铺垫，经历方法“多样性”到“普适性”的归纳过程

【教学片段1】

幼儿园购进了12箱迷你南瓜，每箱23个，一共有多少个？

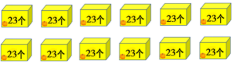
师：23×12的结果是多少，你能想办法解决这个问题吗？请你在图上圈一圈，用学过的算式表达出你的思考过程。

生1：把12拆成4×3，先算4箱个数，再算3个4箱个数，算式是23×4×3。

生2：把12拆成6×2，先算出6箱个数，再算2个6箱，算式是23×6×2。

生3：把12拆成10和2，先分别算出10箱和2箱的个数，然后把两次结果相加，算式是23×10+23×2。

……

师：这些不同的方法背后，有没有相同的地方？

生：都是在把两位数乘两位数转化成两、三位数乘一位数和两位数乘整十数加以解决。

师：如果要求13箱迷你南瓜一共几个，该怎么算？

生：把13拆成10和3，先分别算出10箱和3箱的个数，然后把两次结果相加，算式是23×10+23×3。

师：为什么不选乘了再乘的方法？

生：13没法拆成几乘几。

师：如果求37箱呢？如果23乘的是任意的两位数，又该怎么算？

师：没错，两位数乘两位数，可以先把其中一个乘数拆分成整十数和一位数，分别与另一个乘数相乘，然后把结果相加，这种“两乘一加”的方法适用于任何两位数乘两位数，具有通用性。

算理是算法的灵魂，如何让学生更好地理解算理，为算法教学做好铺垫？教学中，教师在两个方面做了小小的调整：一是开放问题情境，把教材的问题情境替换成散落的12箱迷你南瓜情境，便于学生在图中圈一圈，写一写，让几何直观与数学抽象建立联结，而且开放性的问题情境更有利于暴露学生的认知差异，让方法呈现多样性，在异中求同的比较分析中深刻感受转化的思想；二是把教材中“每箱24个”替换成“每箱23个”，让学生把目光聚焦在乘数的拆分上，随着箱数由合数变成质数，由质数变成任意两位数，学生经历了从“多样性”到“普适性”的归纳过程，深刻理解了计算两位数乘两位数利用乘法分配律进行转化的通用性，为竖式教学作好铺垫。

2. 合作交流，经历算法“个性化”到“规范化”的体验过程

【教学片段2】

师：以“23×12”为例，你能把“两乘一加”的口算过程在一个竖式上体现出来吗？

学生自主探究，教师逐一呈现学生作品，引导合作交流。

 

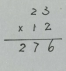
师：（呈现图4）大家觉得这个竖式怎么样？

生：这个竖式不能体现“两乘一加”的思考过程。

师：（呈现图5）这个竖式有点意思。我们邀请作品的主人上台，接受大家的咨询。看懂的就提个问题考考他，看不懂的就提个问题请教他。

生：46是哪来的？求的是几箱的个数？

生：230哪来的？1乘23不是23吗，怎么会是230呢？ 230算的是几箱的个数？

生：为什么第一个乘数要先乘第二个乘数的个位，再乘十位？如果先乘十位，再乘个位，可以吗？

……

师：（呈现图6）看这位同学的作品，加号省去还不去说他，居然把0也给省掉了，你们认为这个0能不能省略不写？

生：不能。如果省略了0，230就变成23了。

生：我反对！一个数写个位，就表示有多少个一；写在十位，就表示有多少个十；写在百位，就表示有多少个百。23的末位写在十位，就表示有23个十。在竖式中，这个0写与不写，不会改变数的大小。

生：刚才的计算过程中，第一次算的是23×2，是两位数乘一位数；第二次算的是23×1，是两位数乘一位数，只不过这里的1是十位上的1。所以得数的末位跟十位对齐就可以了。

生4：这里的0省略不写，更能体现数学的简洁之美。

……

【教学片段3】

师：同学们有没有思考过这样一个问题，除了今天学的这种笔算方法，还有别的方法吗？下面这些算法，你能看懂吗？有什么想法？

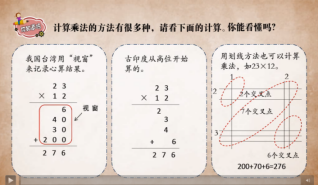
在本环节的教学中，教师设置了挑战性问题，要求学生把“两乘一加”的口算过程用一个竖式表达，开放的问题情境为学生的个性化表达提供了机会。在交流环节，呈现 “看见0”的初始乘法竖式（见图5），让口算、笔算和情境图同屏呈现，实现算理和算法的沟通，以及运算顺序规定的溯源；再引出“省略0”的规范乘法竖式（见图6），循理入法，以理驭法，学生更能体会“压缩”的规范竖式的好处，实现了算法表达个性化到规范化的自然过渡。片段3的史料链接，使得位值原理、程序化规则、转化思想、数学简洁之美，从内隐走向外显，学生感受到数学好玩、好妙、好美，逻辑思考、反思、解释和证明的能力自然生长。

3. 抽象建模，感悟法则由“特殊”到“一般”的衍生过程

【教学片段4】

师：以前学了多位数乘一位数，今天学的是两位数乘两位数，今天学的和以前学的有什么区别和联系吗？

生：多位数乘一位数只要用个位乘第一个乘数，两位数乘两位数要先用个位乘第一个乘数，再用十位乘第一个乘数，要乘两次再相加。

生：都是从个位乘起，从右往左依次乘，都要求数位对齐。

生：都用到了转化的思想。多位数乘一位数计算是把它转化成一位数乘一位数加以解决，两位数乘两位数转化成两次两位数乘一位数。

师：两位数乘两位数同学们会算了，大胆想象一下，你还会算几位数乘几位数？

生：三位数乘两位数，四位数乘两位数，三位数乘三位数……

师：别吹牛，来个简单点的！123×22怎么算？（生答略）

师：如果是任意多位数乘两位数呢？

生：不管是几位数乘两位数，都可以把第一个乘数看作一个整体，先用第一个乘数去乘第二个乘数个位上的数，得到的是几个一，积的末位和个位对齐；再用第一个乘数去乘第二个乘数十位上的数，得到的是几个十，积的末位和十位对齐。

师：如果是三位数乘三位数呢？多位数乘多位数呢？

生：多位数乘多位数与两位数乘两位数一样，都是用第一个乘数先去乘第二个乘数的个位，然后乘十位、百位，一位一位乘下去，乘到第二个乘数哪一位，积末位就对齐哪一位，最后把所有积相加。

教师同步演示如下：

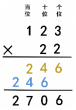
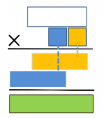
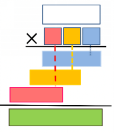
从两位数乘一位数到两位数乘两位数是一个质变的过程，因此两位数乘两位数是学习乘法的一个关键节点，以后学习乘数是三、四位数的乘法只是一个量变的过程。本环节让学生由两位数乘两位数类比迁移到多位数乘多位数，逐步抽象建模，扩展和建立范畴的聚集，让学生在“具体”到“抽象”、“特殊”到“一般”的推理中，实现模式的感知与固化，促进了数学理解深度、广度和完整度的相互关联。

要想提高数学运算意义理解的能力，教师需创设联结，用系统的视角，处理好认知与情感、算理和算法、结果与过程、知识与文化的关系；用长程的眼光，处理好“长线”与“短线”的关系，对数学课程进行整体性，贯通性设计，促进学生数学素养的提升！

【参考文献】